Algebra (Part 4)
Imaginary Numbers
In my previous article, Algebra (Part 3), we met imaginary unit, \(i\). We have imaginary numbers because they provide solutions to equations that are unsolvable with real numbers alone, like \(x^{2}+1=0\).
- \(i = \sqrt{-1}\)
- \(i^2 = -1\)
- \(i^3 = i^2 \cdot i = -1 \cdot i = -i\)
- \(i^4 = i^2 \cdot i^2 = -1 \cdot -1 = 1\)
- \(i^5 = i^4 \cdot i = 1 \cdot i = i\)
- \(i^6 = i^4 \cdot i^2 = 1 \cdot -1 = -1\)
- \(i^7 = i^4 \cdot i^3 = 1 \cdot -i = -i\)
- \(i^8 = i^4 \cdot i^4 = 1 \cdot 1 = 1\)
- \(i^{20} = (i^4)^5 = 1^5 = 1\)
- \(i^{227} = (i^4)^{56} \cdot i^3 = 1^{56} \cdot i^3 = 1 \cdot -i = -i\)
- \(i^{2016} = (i^4)^{504} = 1^{504} = 1\)
From those statements, we got these statements.
- \((4i)^2 = 16 \cdot -1 = -16\)
- \(\sqrt{-16} = \sqrt{16 \cdot -1} = 4i\)
\[\text{For } a \gt 0, \sqrt{-a} = i\sqrt{a}\]
- \(\sqrt{-25} = i\sqrt{25} = i \cdot 5 = 5i\)
- \(\sqrt{-24} = i\sqrt{24} = i\sqrt{4 \cdot 6} = i\sqrt{4} \cdot \sqrt{6} = i \cdot 2 \cdot \sqrt{6} = 2i \sqrt{6}\)
Complex Numbers
\[a + bi\]
A complex number is a number that combines a real number and an imaginary number, written in the form \(a+bi\), where \(a\) is the real part and \(bi\) is the imaginary part.
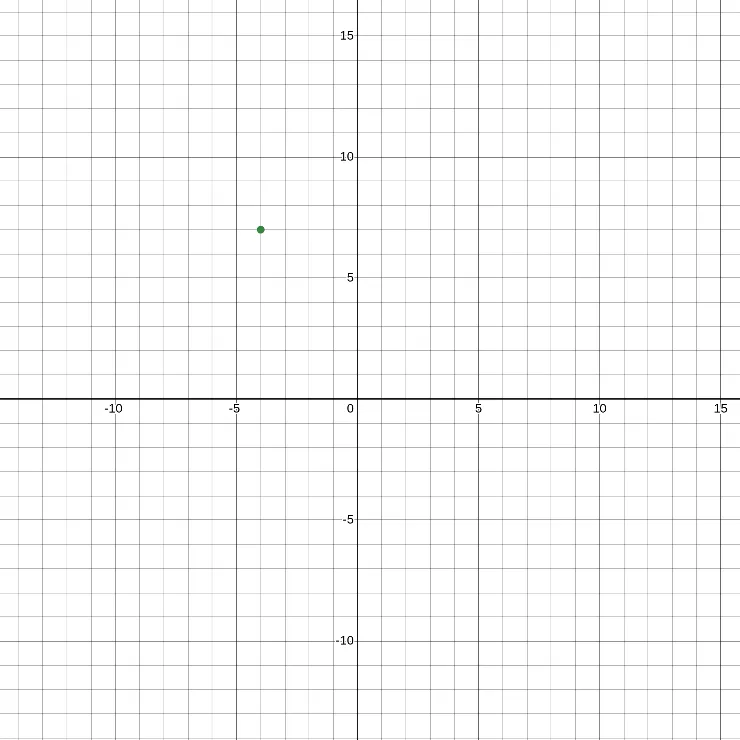
\(-4 + 7i\) is an example of a complex number. If we want to plot it, the point is in (-4, 7). In general, the complex number, \(a + bi\), corresponds to the point \((a, b)\) in the complex plane.
Operations
| Operation | Formula |
|---|---|
| Addition | \((a_1+b_1i)+(a_2+b_2i)=(a_1+a_2)+(b_1+b_2)i\) |
| Subtraction | \((a_1+b_1i)-(a_2+b_2i)=(a_1-a_2)+(b_1-b_2)i\) |
| Multiplication | \((a_1+b_1i)\cdot(a_2+b_2i)=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\) |
| Division | \(\frac{(a_1+b_1i)}{(a_2+b_2i)} = \frac{(a_1+b_1i)}{(a_2+b_2i)} \cdot \frac{(a_2-b_2i)}{(a_2-b_2i)} = \frac{(a_1+b_1i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} = \frac{(a_1a_2 + b_1b_2)+(b_1a_2 - a_1b_2)i}{(a_2)^2+(b_2)^2}\) |
Operation Examples
Addition
\((21 + 2i) + (13 + 8i) = (21 + 13) + (2 + 8)i = 34 + 10i\)
Subtraction
\((7 - 10i) - (3 + 30i) = (7 - 3) - (-10 - 30)i = 4 - 40i\)
Multiplication
\begin{aligned} (1 + i) \cdot (3 - 5i) &= 1 \cdot 3 + 1 \cdot -5i + i \cdot 3 + i \cdot -5i \\\\ &= 3 - 5i + 3i - 5i^2 \\\\ &= 3 - 2i - 5 \cdot -1 \\\\ &= 8 - 2i \end{aligned}
Division
\begin{aligned} \frac{3 + 2i}{1 - i} &= \frac{3 + 2i}{1 - i} \cdot \frac{1 + i}{1 + i} \\\\ &= \frac{(3 + 2i)(1 + i)}{(1 - i)(1 + i)} \\\\ &= \frac{3 + 3i + 2i + 2i^2}{1^2 - i^2} \\\\ &= \frac{3 + 5i - 2}{1 + 1} \\\\ &= \frac{1 + 5i}{2} \\\\ &= \frac{1}{2} + \frac{5}{2}i \end{aligned}
Sign of Average (Rate) of Change (ARC) of Polynomials
In my previous article, Algebra (Part 2), we met Average of Change. Using the same equation, we can determine whether the average of the change is positive, negative, or zero.
| Sign | Meaning | Behavior |
|---|---|---|
| Positive \((\gt 0)\) | \(f(b) \gt f(a)\) | the graph goes up as \(x\) increases |
| Negative \((\lt 0)\) | \(f(b) \lt f(a)\) | the graph goes down as \(x\) decreases |
| Zero \((= 0)\) | \(f(b) = f(a)\) | the graph is flat |
Example
\[h(t) = (t + 3)^2 + 5\]
From the function above, let's find the sign of these intervals below.
| Interval | Calculation | Sign |
|---|---|---|
| \(1 \le t \le 4\) |
|
\(54 \gt 21\), positive |
| \(-4 \le t \le -3\) |
|
\(5 \lt 6\), negative |
Polynomial Arithmetic
In my previous article, Algebra (Part 3), we met a Polynomial. In this article, we will cover more about Polynomial Arithmetic, especially Addition, Subtraction, and Division.
To add and subtract polynomials, combine like terms (terms with the same variables and exponents) by adding or subtracting their coefficients. For subtraction, distribute the negative sign to each term in the second polynomial before combining like terms, which is the same as adding the opposite of each term.
Addition
\[P(x) + Q(x) = (P + Q)x\]
Example
\begin{aligned} (-3y^2 - 5y - 2) + (-7y^2 + 5y + 2) &= (-3 - 7)y^2 + (-5 + 5)y + (-2 + 2) \\\\ &= -10y^2 + 0y + 0 \\\\ &= -10y^2 \end{aligned}
Subtraction
\[P(x) - Q(x) = (P - Q)x\]
Example
\begin{aligned} (f^3 - 5f + 25) - (4f^2 - 12f + 9) &= f^3 - 4f^2 + (-5 - (-12))f + (25 - (+9)) \\\\ &= f^3 - 4f^2 + (-5 + 12)f + (25 - 9) \\\\ &= f^3 - 4f^2 + 7f + 16 \end{aligned}
Division
Polynomial division is an algorithm used to divide one polynomial by another polynomial of the same or lower degree. The Long Division method helps illustrate and understand this process more clearly. In some examples, there is another version of Long Division.
\begin{aligned} f(x) &= d(x) \cdot q(x) + r(x) \\\\ \frac{f(x)}{d(x)} &= q(x) + \frac{r(x)}{d(x)} \\\\ f(x) &= (x−c)q(x)+r \end{aligned}
- \(f(x)\) = dividend
- \(d(x)\) = divisor
- \(q(x)\) = quotient
- \(r(x)\) = remainder
If a polynomial \(f(x)\) is divided by \((x−c)\), then the remainder of that division is equal to \(f(c)\). It is called Remainder Theorem.
Example
-
-
\(\frac{x^2 + 3x + 2}{x + 1} = \frac{(x + 2)(x + 1)}{x + 1} = x + 2, x \neq -1\)
\(x \neq -1\) means as long as \(x\) is not equal to \(-1\).
- \( \begin{array}{rll} x + 2 \\ x + 1 \enclose{longdiv}{x^2 + 3x + 2} \\ \underline{x^2 + x \phantom{xxxx}} \\ 2x + 2 \\ \underline{2x + 2} \\ 0 \end{array} \)
-
- \(\frac{4x^3 + x^2}{x} = \frac{x(4x^2 + x)}{x} = 4x^2 + x\)
- \(\frac{2x^3 + 7}{x} = \frac{2x^3}{x} + \frac{7}{x} = 2x^2 + \frac{7}{x}\)
- \(\frac{x^2 - 9}{x - 3} = \frac{(x - 3)(x + 3)}{x - 3} = x + 3\)
-
- \(\frac{x^2 + 5x + 8}{x + 2} = \frac{x^2 + 5x + 6 + 2}{x + 2} = \frac{(x + 2)(x + 3)}{x + 2} + \frac{2}{x + 2} = (x + 3) + \frac{2}{x + 2}, x \neq -2\)
- \( \begin{array}{rll} x + 3 \\ x + 2 \enclose{longdiv}{x^2 + 5x + 8} \\ \underline{-x^2 - 2x \phantom{xxx}} \\ 3x + 8 \\ \underline{-3x - 6} \\ 2 \end{array} \)
-
- \(\frac{x^2 + 1}{x + 2} = \frac{x^2 - 4 + 5}{x + 2} = \frac{(x + 2)(x - 2)}{x + 2} + \frac{5}{x + 2} = (x - 2) + \frac{5}{x + 2}, x \neq -2\)
- \( \begin{array}{rll} x - 2 \\ x + 2 \enclose{longdiv}{x^2 + 0x + 1} \\ \underline{-x^2 - 2x \phantom{xxx}} \\ -2x + 1 \\ \underline{2x + 4} \\ 5 \end{array} \)
-
\(P(x)=x^4-2x^3-3x^2+4\)
What is the remainder when \(P(x)\) is divided by \((x - 3)\)?
\( \begin{aligned} P(3) &= (3)^4 - 2(3)^3 - 3(3)^2 + 4 \\ &= 81 - 54 - 27 + 4 \\ &= (81 - 54) - 27 + 4 \\ &= 27 - 27 + 4 \\ &= 4 \end{aligned} \)
-
Find the value of \(c\) so that \((x + 1)\) is a factor of the polynomial \(p(x)\).
\(p(x) = 5x^4+7x^3 -2x^2 -3x + c\)
\( \begin{aligned} 5(-1)^4+7(-1)^3 -2(-1)^2 -3(-1)+c&=0 \\\\ 5-7-2+3+c&=0 \\\\ -1 +c&=0 \\\\ c&=1 \end{aligned} \)
Greatest Common Factor (GCF) of Monomials
In Pre-Algebra, we already knew about GCF. GCF of monomials is similar, but we have variables here. Here are examples.
-
GCF of \(6a\), \(8a^2\), and \(14\) is \(\mathbf{2}\).
- \(6a = ({\color{gold}{2}})(3)(a)\)
- \(8a^2 = ({\color{gold}{2}})(2)(2)(a)(a)\)
- \(14 = ({\color{gold}{2}})(7)\)
-
GCF of \(30b^2\), \(80b^2\), and \(20b^3\) is \(\mathbf{10b^2}\).
- \(30b^2 = ({\color{gold}{2}})(3)({\color{gold}{5}})({\color{gold}{b}})({\color{gold}{b}})\)
- \(80b^2 = ({\color{gold}{2}})(2)(2)(2)({\color{gold}{5}})({\color{gold}{b}})({\color{gold}{b}})\)
- \(20b^3 = ({\color{gold}{2}})(2)({\color{gold}{5}})({\color{gold}{b}})({\color{gold}{b}})(b)\)
\({\color{gold}{(2)(5)(b)(b)}} = \mathbf{10b^2}\)
Factoring Polynomials by the Distributive Property
\[x(a + b) = ax + bx\]
- Find the GCF.
- Divide each term by the GCF.
These examples make it clear.
- \(6x^3 + 8x^2 - 4x = 2x(\frac{6x^3}{2x} + \frac{8x^2}{2x} - \frac{4x}{2x}) = 2x(3x^2 + 4x - 2)\)
- \(14x^2 + 28x^5 = 14x^2(\frac{14x^2}{14x^2} + \frac{28x^5}{14x^2}) = 14x^2(1 + 2x^3)\)
Factoring Higher Degree Polynomials
More examples in Higher Degree Polynomials.
- \begin{aligned} 5x^4 - 20x^3 + 20x^2 &= 5x^2(x^2 - 4x + 4) \\\\ &= 5x^2(x - 2)^2 \end{aligned}
- \begin{aligned} (x^2 + x - 6)(2x^2 + 4x) &= (x + 3)(x - 2)(2x(x + 2)) \\\\ &= 2x(x + 2)(x + 3)(x - 2) \end{aligned}
Quadratic Patterns
In my previous article, Algebra (Part 3), section Difference of Squares and Perfect Squares.
Let me rewrite the patterns here with \(U\) and \(V\). \(U\) and \(V\) are either constant integers or single-variable expressions.
\begin{aligned} (U + V)^2 &= U^2 + 2UV + V^2 \\\\ (U - V)^2 &= U^2 - 2UV + V^2 \\\\ (U + V)(U - V) &= U^2 - V^2 \end{aligned}
If the expression can't use any of those patterns, then we can't use any of the patterns, which means the expression is not factorable. Here are examples.
-
\((x + 7)^2 + 2y(x + 7) + y^2 = (U + V)^2\)
- \(U = (x + 7)\)
- \(V = y\)
- \(x^4+10x+25\) is not factorable.
-
\(16x^4 - 25 = (U + V)(U - V)\)
- \(U = 4x^2\)
- \(V = 5\)
Geometric Series

A geometric sequence is a list of numbers where each term is obtained by multiplying the previous one (starting with the first term, \(a\)) by a fixed number called the common ratio \((r)\).
Sum of Geometric Series
\begin{aligned} S_n &= a + ar + ar^2 + \ldots + ar^{n−1} \\\\ rS_n &= \phantom{a + {}} ar + ar^2 + \ldots + ar^{n} \\\\ −rS_n &= \phantom{a {}} − ar − ar^2 − \ldots −ar^{n} \\\\ S_n - rS_n &= a - ar^{n} \\\\ S_n(1 - r) &= a(1 - r^{n}) \\\\ S_n &= \frac{a(1 - r^{n})}{1 - r} \end{aligned}
Examples
- \begin{aligned} 3 + 6 + 12 + 24 + 48 &= \frac{a(1 - r^{n})}{1 - r} \\\\ &= \frac{3(1 - 2^{5})}{1 - 2} \\\\ &= \frac{3(1 - 32)}{-1} \\\\ &= \frac{3(-31)}{-1} \\\\ &= \frac{-93}{-1} \\\\ &= 93 \end{aligned}
-
The sum of the first \(3\) terms of a geometric series is \(171\), and the common ratio is \(\frac{2}{3}\).
What is the first term of the series?
\begin{aligned} 171 &= \frac{a(1 - (\frac{2}{3})^{3})}{1 - \frac{2}{3}} \\\\ &= \frac{a(1 - \frac{8}{27})}{1 - \frac{2}{3}} \\\\ &= \frac{a(\frac{19}{27})}{\frac{1}{3}} \\\\ 57 &= a (\frac{19}{27}) \\\\ 57 (\frac{27}{19}) &= a \\\\ 81 &= a \end{aligned}
-
Find the sum of the first 8 terms in the following geometric series, \(2 + 8 + 32 + \dots\).
Do not round your answer.
\begin{aligned} a &= 2 \\\\ r &= \frac{ar}{a} = \frac{8}{2} = 4 \\\\ S_8 &= \frac{2(1 - 4^8)}{1 - 4} = \frac{2(1 - 65536)}{1 - 4} = \frac{2(-65535)}{-3} = \frac{-131070}{-3} = 43690 \end{aligned}
-
A monkey is swinging from a tree. On the first swing, she passes through an arc of \(10m\). With each swing, she passes through an arc \(\frac{9}{10}\) of the length of the previous swing. What is the total distance the monkey has traveled when she completes her 25th swing? Round your final answer to the nearest meter.
\begin{aligned} a &= 10 \\\\ r &= \frac{9}{10} = 0.9 \\\\ S_{25} &= \frac{10(1 - 0.9^{25})}{1 - 0.9} = \frac{10(1 - 0.0717)}{1 - 0.9} = \frac{10(0.9283)}{0.1} = \frac{9.283}{0.1} = 92.83 \\\\ &\approx 93 \end{aligned}
Reference
The primary reference is Khan Academy, with assistance from ChatGPT and Gemini as well.