Algebra (Part 2)
I suggest you read my previous article about Pre-Algebra before we go any further.
Functions
In Pre-Algebra, I already introduced Functions. In this section, let's talk about the average rate of change of functions.
Average Rate of Change
\[\frac{f(b) - f(a)}{b - a}\]
The \(a\) and \(b\) from the expression above are from the interval, \(a \le x \le b\). Here are examples.
-
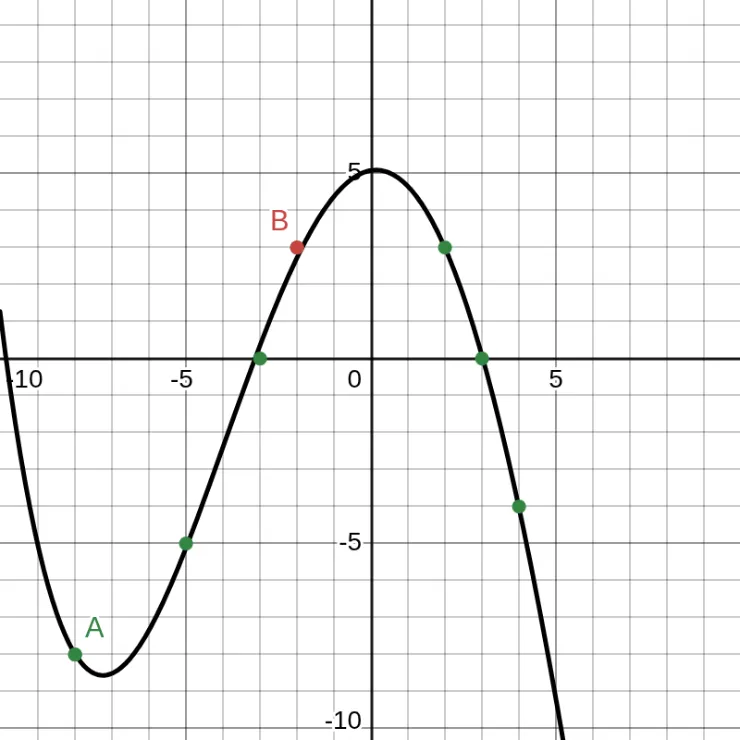
\(-8 \le x \le -2\). (-8, -8) and (-2, 3). What is the average rate of change of \(g\) over the interval \(-8\leq x\leq -2\) from the graph above?
We can see from the graph above that \(g(-8)=-8\) and \(g(-2)=3\). So, the average of change is \(\frac{g(-2) - g(-8)}{-2 - (-8)} = \frac{3 - (-8)}{6} = \frac{11}{6}\).
-
What is the average rate of change of \(f(x)= x^2 + 10\) over the interval \(-2\leq x \leq 3\)?
From the mentioned interval, we can see that \(a = -2\) and \(b = 3\).
- \(f(a) = f(-2) = (-2)^2 + 10 = 14\)
- \(f(b) = f(3) = 3^2 + 10 = 19\)
So, the average of change is \(\frac{19 - 14}{3 - (-2)} = \frac{5}{5} = 1\).
-
\(T(t)\) is the temperature in Windhoek, Namibia (measured in degrees Celsius) when it's \(t\) hours after midnight on a given day.
\(t\) \(T(t)\) 6 19 9 25 13 31 Let's calculate each range from the table above.
- \(\frac{T(9) - T(6)}{9 - 6} = \frac{25 - 19}{9 - 6} = \frac{6}{3} = 2\)
- \(\frac{T(13) - T(9)}{13 - 9} = \frac{31 - 25}{13 - 9} = \frac{6}{4} = 1\frac{2}{4} = 1\frac{1}{2}\)
Since \(2 \gt 1\frac{1}{2}\), the answer is between 6 and 9.
Inverse Functions
\[f(a) = b \iff f^{-1}(b) = a\]
For example, we use this equation, \(C = \frac{5}{9}(F - 32)\), to convert degrees Celsius to Fahrenheit. If we invert the function, to convert degrees Fahrenheit to Celsius, the function will be like this: \(F = \frac{9}{5}C + 32\).
Sequences
We all knew about sequences, right? A sequence is an ordered list of objects, usually numbers, that follow a specific pattern or rule. These objects are called terms, and the sequence can be finite (having a limited number of terms) or infinite (extending without end).
Arithmetic Sequences
An arithmetic sequence is a sequence of numbers where the difference between any two successive terms is constant. This constant difference is called the common difference. We get the next number in the sequence by adding or subtracting the same value. Here are examples.
- \(2, 8, 14, 20, \unicode{0x2026}\), the common difference is 6.
- \(5, 2, -1, 4, \unicode{0x2026}\), the common difference is -3.
- \(1, 1\frac{1}{3}, 1\frac{2}{3}, 2, \unicode{0x2026}\), the common difference is \(\frac{1}{3}\).
Formula
A formula is a concise way to express a relationship between different quantities using symbols and operators. It's essentially a rule or a recipe that allows you to calculate a specific value or solve a problem by substituting known values into the equation.
There are two kinds of formulas in Arithmetic Sequences: Recursive and Explicit.
Recursive Formula

A recursive formula defines a sequence by specifying the first term and a rule for generating subsequent terms. Here is an example.
- \(b(1) = 5\)
- \(b(n) = b(n - 1) + 9\)
- \(b(4) = \text{?}\)
We need a table to answer \(b(4)\). A table that calculates the previous sequences.
| \(b(n)\) | \(b(n - 1) + 9\) | ||
|---|---|---|---|
| \(b(1)\) | \(= -5\) | ||
| \(b(2)\) | \(b(1) + 9\) | \(-5 + 9\) | \(= 4\) |
| \(b(3)\) | \(b(2) + 9\) | \(4 + 9\) | \(= 13\) |
| \(b(4)\) | \(b(3) + 9\) | \(13 + 9\) | \(= 22\) |
Explicit Formula
\[k + d(n - 1)\]
An explicit formula defines each term of a sequence directly in terms of its position. Here is an example.
- \(b(n) = -5 + 9(n - 1)\)
- \(b(10) = -5 + 9(10 - 1) = -5 + 9(9) = -5 + 81 = 76\)
As you can see, the explicit formula goes straight to the formula; no table is needed to calculate the previous sequence.
Finding the Explicit Formula
What is the explicit formula of the sequence \(12, 7, 2,\unicode{0x2026}\)? The first term or \(k\) is 12 and the common difference or \(d\) is 5. So, the explicit formula is \(12 - 5(n - 1)\).
\[k + dn\]
Let's convert \(k + d(n - 1)\) to \(k + dn\).
- \(12 - 5(n - 1)\)
- \(12 - 5n + 5\)
- \(17 - 5n\)
A Recursive Formula to an Explicit Formula
- \(b(1) = -22\)
- \(b(n) = b(n - 1) + 7\)
From that recursive formula, we got that the first term is -22 and the common difference is 7. So, the exclusive formula is \(b(n) = -22 + 7(n - 1)\).
An Explicit Formula to a Recursive Formula
\(g(n) = -11 - 8(n - 1)\). We can see that the first term is -11 and the common difference is -8. The recursive formula is below.
- \(g(1) = -11\)
- \(g(n) = g(n - 1) - 8\)
\(h(n) = 1 + 4n\). We need to find the first two terms because the formula is not given in the standard explicit form.
- \(h(1) = 1 + 4 \cdot 1 = 1 + 4 = 5\). This is the first term.
- \(h(2) = 1 + 4 \cdot 2 = 1 + 8 = 9\). The common difference is \(h(n) - h(n - 1) = h(2) - h(1) = 9 - 5 = 4\).
So, the recursive formula of the \(h(n) = 1 + 4n\) is below.
- \(h(1) = 5\)
- \(h(n) = h(n - 1) + 4\)
Geometric Sequences
A geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a constant value called the common ratio \((r)\).
\[a(n) = k \cdot r^{n-1}\]
The formula above is the explicit formula of a geometric sequence. Here is the recursive version.
- \(a(1) = k\)
- \(a(n) = a(n - 1) \cdot r\)
Recursive Formula
What is the recursive formula of the sequence \(\frac{1}{2}, 2, 8, \ldots\)? We can see that the first term is \(\frac{1}{2}\) and the common ratio is 4. So, the recursive formula is below.
- \(a(1) = \frac{1}{2}\)
- \(a(n) = a(n - 1) \cdot 4\)
Explicit Formula
The explicit formula of the sequence \(\frac{1}{2}, 2, 8, \ldots\) is \(\frac{1}{2} \cdot 4^{n-1}\).
Graph with Absolute Value
We already knew about absolute value with its symbol in Pre-Algebra. Now, let's graph it.
\[f(x) = a|x - h| + k\]
The equation above is the general form of an absolute value. The \(a\) determines the vertical stretch or compression and whether the graph opens upwards or downwards. The \(h\) determines the horizontal shift (left or right), and the \(k\) determines the vertical shift (up or down).
Here is an example of \(f(x) = -3|x + 3| - 2\).
_=_-3_x_+3__-2.webp)
- The value of \(a\) is -3. So the graph opens downwards with a slope of -3.
- The value of \(h\) is also -3 (because \(x - (-3) = x + 3\)). So the vertex of the graph is shifted 3 units to the left, or \(x = -3\).
- The value of \(k\) is -2. So the vertex of the graph is shifted 2 units to the bottom, or \(y = -2\).
Piecewise Functions
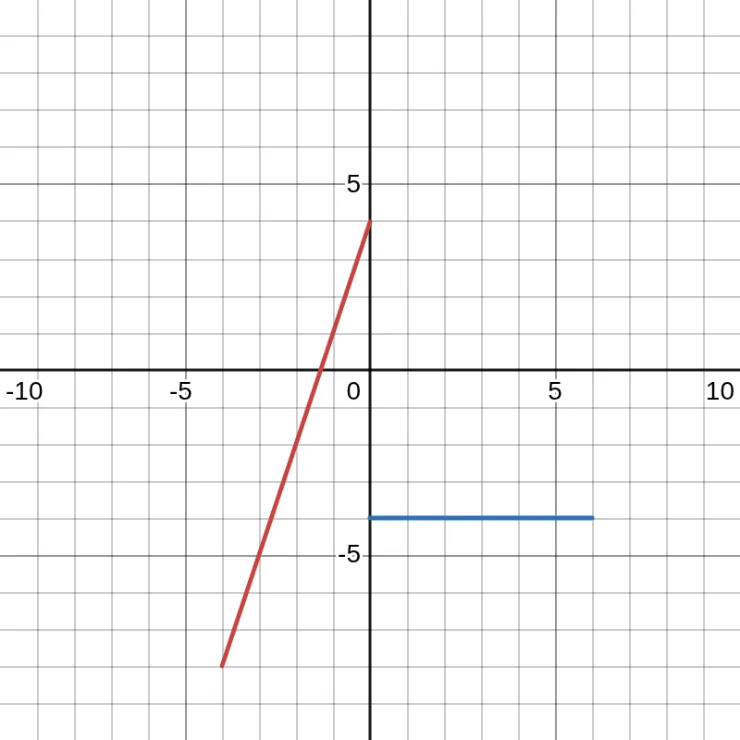
A piecewise function is a function defined by multiple sub-functions, each applying to a specific interval of the main function's domain. Here is an example
\[f(x) = \begin{cases} 3x + 4, & -4 \le x \lt 0 \\ -4, & 0 \le x \le 6 \end{cases}\]
Higher Order Roots
We already knew about square and cube roots since Pre-Algebra. This section introduced higher-order roots.
- \(\sqrt[4]{16} = 2 \iff 2^4 = 16\)
- \(\sqrt[5]{1024} = 4 \iff 4^5 = 1024\)
- \(\sqrt[9][512] = 2 \iff 2^9 = 512\)
The pattern is the same as square and cube roots. But we called it \(n^{\text{th}}\) roots.
Simplifying Square Roots
Here are the steps:
- Prime Factorization Find the prime factors of the number under the square root (radicand).
- Pairing Factors Look for pairs of identical prime factors.
- Extracting Factors: For each pair, take one factor out of the square root.
- Remaining Factors: Any factors that don't have a pair stay inside the square root.
- Simplifying: Multiply the factors outside the radical and the factors inside the radical separately.
Here are examples.
- \(\begin{aligned} \sqrt{12}&=\sqrt{2 \cdot 2 \cdot 3} \\\\ &=\sqrt{2^2\cdot 3} \\\\ &=\sqrt{2^2}\cdot\sqrt{3} \\\\ &=2\sqrt3 \end{aligned}\)
- \(\begin{aligned} \sqrt{72}&=\sqrt{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} \\\\ &=\sqrt{2^3\cdot 3^2} \\\\ &=\sqrt{2^2}\cdot\sqrt{3^2}\cdot\sqrt{2} \\\\ &=2\cdot 3\cdot\sqrt2 \\\\ &=6\sqrt2 \end{aligned}\)
Simplifying square roots with variables
Here is an example.
\(\begin{aligned} \sqrt{20x^8}&=\sqrt{2 \cdot 2 \cdot 5\cdot x^8} \\\\ &=\sqrt{2^2\cdot 5\cdot x^8} \\\\ &=\sqrt{2^2}\cdot \sqrt{5} \cdot \sqrt{x^8} \\\\ &=2\cdot \sqrt{5} \cdot x^4 \\\\ &=2x^4\sqrt{5} \end{aligned}\)
Here is another challenging example.
\(\begin{aligned} 2\sqrt{7x}\cdot 3\sqrt{14x^2}&=2\cdot 3\cdot\sqrt{7x}\cdot\sqrt{14x^2} \\\\ &=6\sqrt{98x^3} \\\\ &=6\sqrt{7^2\cdot x^2\cdot 2x} \\\\ &=6\sqrt{7^2}\cdot\sqrt{x^2}\cdot\sqrt{2x} \\\\ &=6\cdot 7\cdot x\sqrt{2x} \\\\ &=42x\sqrt{2x} \end{aligned}\)
General Rules of Exponents and Radicals
From the example above, you may have wondered why \(\sqrt{x^8} = x^4\)? That came from the general rule of exponents and radicals.
\[\sqrt[n]{a^m} = a^{\frac{m}{n}}\]
General Rules of Exponents
- Product of powers: \(a^m \cdot a^n = a^{m+n}\)
- Quotient of powers: \(\frac{a^m}{a^n} = a^{m-n}\)
- Power of a power: \((a^m)^n = a^{mn}\)
- Power of a product: \((ab)^n = a^n \cdot b^n\)
- Power of a quotient: \((\frac{a}{b})^n = \frac{a^n}{b^n}\)
General Rules of Radicals (\(\sqrt{}\))
- Product of radicals: \(\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab}\)
- Quotient of radicals: \(\sqrt[n]{a} / \sqrt[n]{b} = \sqrt[n]{\frac{a}{b}}\)
- Power of a radical: \((\sqrt[n]{a})^m = \sqrt[n]{a^m} = a\frac{m}{n}\)
Exponential Growth
Exponential growth describes a pattern where a quantity increases at an accelerating rate, becoming increasingly rapid over time. In an exponential relationship, the \(y\)-values have equal ratios.
Here is an example.
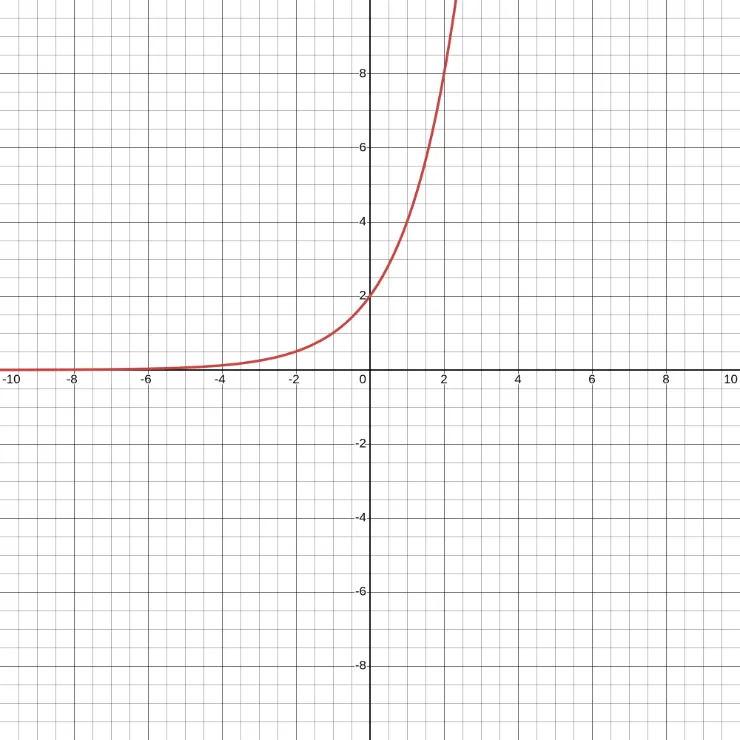
From the graph above, we get the table below.
| \(x\) | \(y\) |
|---|---|
| -2 | \(\frac{1}{2}\) |
| -1 | 1 |
| 0 | 2 |
| 1 | 4 |
| 2 | 8 |
From the table above, we can see that to get the next \(y\), we need to multiply the current \(y\) by 2. This is the difference between exponential growth and linear growth.
Exponential Decay
Exponential decay is a process where a quantity decreases over time at a rate proportional to its current value. In short, Exponential Decay is the opposite of Exponential Growth. It is decreasing faster because the next value of \(y\) gets multiplied by a fraction.
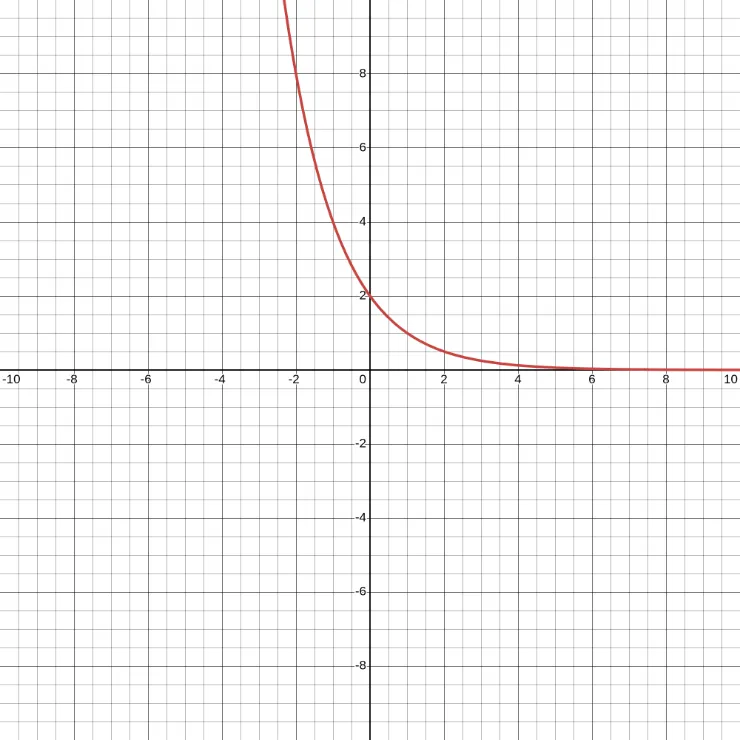
From the graph above, we get the table below.
| \(x\) | \(y\) |
|---|---|
| -2 | 8 |
| -1 | 4 |
| 0 | 2 |
| 1 | 1 |
| 2 | \(\frac{1}{2}\) |
From the graph and the table above, we can see that \(y\) is decreasing because it was multiplied by \(\frac{1}{2}\).
References
- Khan Academy
- https://www.cuemath.com/algebra/exponent-rules/
- https://www.cuemath.com/algebra/rational-exponents/