Pre-Algebra

July 5, 2025

Pre-Algebra is a pack of maths that you need to master for the study of Algebra. You already met these maths in middle school, right?

I want to talk about this mathematics in one article. In case you forgot any terms or equations in Pre-Algebra, you can open this article as your notes.

I would also like to thank Khan Academy for being my primary reference for this article. I recommended that my young brother and sister study maths there because it is free and easy to learn. The way Khan Academy teaches makes the subject easy to understand.

Before taking Algebra, of course, you need to be able to do basic arithmetic operations such as Addition, Subtraction, Multiplication, and Division. You should be able to perform these operations on integers, fractions, and decimals.

An integer is a whole number (not a fraction or decimal) that can be positive, negative, or zero. E.g., -3, 0, 5, and 100.

The absolute value is a number that is the distance from 0 on the number line, which always produces a non-negative value. The absolute value is written with the symbol $|x|$ where $x$ is the number. Here are some examples.

$|-3| = 3$
$|3| = 3$

Ratios vs Proportions vs Fractions vs Decimals vs Percents

I think there is no better explanation than examples to explain Ratio, Proportion, Fraction, Decimal, and Percent.

Ratio	Proportions			Fraction	Decimal	Percent
1:2	2:4	3:6	4:8	$\frac{1}{2}$	0.5	50%
3:2	6:4	9:6	12:8	$1\frac{1}{2}$	1.5	150%
3:4	6:8	9:12	12:16	$\frac{3}{4}$	0.75	75%

Have you understood ratios and proportions from the examples above? A ratio is a comparison of two or more numbers that indicates their relative sizes. A proportion is an equation stating that two ratios are equal.

Rates

Now that you know about ratios and proportions, you can calculate the unit rate. A rate is a ratio that compares two quantities with different units of measurement. A unit rate of two quantities in a ratio is the number of units of the first quantity for every 1 unit of the second quantity. Here are examples.

Frances can complete 91 oil changes in 7 days. How many oil changes can Frances complete in 11 days?

$91 \div 7 = 13$
$13 \times 11 = 143$

At the market, 5 light bulbs cost $9.85. How much do 7 light bulbs cost?

$9.85 \div 5 = 1.97$
$1.97 \times 7 = 13.79$

PEMDAS

PEMDAS is an acronym that helps you remember the order of operations.

Parentheses
Exponents
Multiplication and Division (from left to right)
Addition and Subtraction (from left to right)

Here are examples.

1. $2 + 12 \div 2 \times 3$
2. $2 + 6 \times 3$
3. $2 + 18$
4. $20$
1. $7 ^ 2 + 3(4 ^ 2 + 3 + 2)$
2. $49 + 3(16 + 3 + 2)$
3. $49 + 3 \times 21$
4. $49 + 63$
5. $112$
1. $8 - (-10 + 8)^2$
2. $8 - (-2)^2$
3. $8 - 4$
4. $4$

Exponents vs Roots

Now that you know about exponents. Let's compare it with (square and cube) roots. The square root of a number is a value that, when multiplied by itself, equals the original number. The symbol for square root is $\sqrt{x}$ (where $x$ is a number), called a radical. The cube root of a number is a value that, when multiplied by itself three times, equals the original number. The symbol for cube root is $\sqrt[3]{x}$ (where $x$ is a number). Here are examples.

$\sqrt{25} = 5$ because $5^2 = 25$
$\sqrt{1} = 1$ because $1^2 = 1$
$\sqrt[3]{125} = 5$ because $5^3 = 125$

Power of 1, 0, and Negative Number

You might think that exponents start with 2. How about the power of 0, 1, and negative numbers? The power of 0 is always 1. The power of 1 is always the number itself. The power of negative numbers is always lower than 1 and greater than 0. Here are examples.

$2^0 = 1$
$2^1 = 2$
$2^{-2} = \frac{1}{2}$

Scientific Notation

Scientific notation is a way to express very large or very small numbers in a more concise and convenient form. It involves representing a number as a product of a number between 1 and 10 (inclusive) and a power of 10. Here are examples.

$245{,}600{,}000{,}000 = 245{,}6 \times 10^9 = 2{,}456 \times 10^{11}$
$0.0002077 = 2.077 \times 10^{-4}$

Factors

A factor of a number is any number that divides evenly into the original number. In other words, if you can divide a number by another number without leaving a remainder, the second number is a factor of the first.

Here is an example. Factors of 12 are: 1, 2, 3, 4, 6, 12. 5, 7, 8, 9, 10, and 11 are not factors of 12 because they don't divide evenly or leave a remainder.

Multiples

A multiple of a number is the result of multiplying that number by an integer. In other words, a multiple of a number is any number that can be divided evenly by the original number.

Here is an example. The multiples of 4 are: 4, 8, 12, 16, 20, 24,... (and so on). They keep increasing by adding numbers, and those numbers are always a multiple of themselves.

Prime Numbers

Prime numbers are numbers with exactly two factors: 1 and the number itself.

Here is an example. 7 is a prime number because its only factors are 1 and 7.

Composite Numbers

A composite number has more than two factors.

Here is an example. 12 is composite because its factors are 1, 2, 3, 4, 6, and 12.

Greatest Common Factor (GCF)

The GCF is the largest number that divides exactly into two or more numbers, but the GCF must always be less than or equal to the smallest number in the pair.

Here is an example.

Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18

The GCF of 12 and 18 is 6. You might think that 216 (12 x 18) is not the GCF of 12 and 18? It is because 216 is larger than 12 (the smallest number of the pair).

Least Common Multiple (LCM)

The LCM is the smallest number that divides exactly into two or more numbers.

Multiples of 4: 4, 8, 12, 16, 20, 24, ...
Multiples of 5: 5, 10, 15, 20, 25, ...

The LCM of 4 and 5 is 20.

Variables and Expressions

Variables in math are symbols, often letters, that represent different values in various situations. In math expressions, terms are the components added or subtracted, factors are the elements multiplied within each term, and coefficients are the numbers multiplying variables. Here are examples.

$9 + 7y$

Terms are 9 and 7y.
In the term 9, the only factor is 9. In the term 7y, the factors are 7 and y.
The coefficient of the term 7y is 7 (the number multiplying the variable y).

Equations

An equation is a statement that two expressions are equal. All equations have an equal sign ($=$). When we see an equation that's not true, we can use the not equal sign ($\neq$) to show that the two expressions are not equal.

$8 + 2 = 5 + 5$
$7 - 2 \neq 7 + 1$

Algebraic Equations

An algebraic equation is a mathematical statement that asserts the equality of two algebraic expressions. It involves variables, constants (fixed numerical values), and algebraic operations (addition, subtraction, multiplication, division, exponents, and roots). Here are examples.

$2x + 3 = 7$
$y^2 - 4 = 0$

One-step Equations

One-step equations are algebraic equations that can be solved with a single operation (addition, subtraction, multiplication, or division). To solve them, you isolate the variable by performing the inverse operation on both sides of the equation. Here are examples.

1. $k - 7 = 16$
2. $k = 16 + 7$
3. $k = 23$
1. $k + 12 = 37$
2. $k = 37 - 12$
3. $k = 25$
1. $4t = 36$
2. $t = \frac{36}{4}$
3. $t = 9$
1. $\frac{x}{7} = 4$
2. $x = 4 \times 7$
3. $x = 28$

Two-step Equations

Two-step equations are algebraic equations that require two operations to solve for the unknown variable. These equations typically involve a combination of addition/subtraction and multiplication/division. The goal is to isolate the variable on one side of the equation by using inverse operations. Here are examples.

1. $43 = 8c - 5$
2. $43 + 5 = 8c$
3. $48 = 8c$
4. $6 = c$
1. $\frac{h}{6} - 1 = 3$
2. $\frac{h}{6} = 3 + 1$
3. $\frac{h}{6} = 4$
4. $h = 4 \times 6$
5. $h = 24$

Inequalities

Symbol	Meaning
$\gt$	Greater than
$\ge$	Greater than or equal to
$\lt$	Less than
$\le$	Less than or equal to

One-step and Two-step Inequalities

One-step and Two-step Inequalities are the same as One-step and Two-step Equations, but Inequalities use inequality symbols like above instead of the equal symbol, and we have to flip the direction of the inequality when we divide or multiply an inequality by a negative number. Here are examples.

1. $-6x \ge -20$
2. $x \le \frac{-20}{-6}$
3. $x \le 3\frac{2}{6}$
4. $x \le 3\frac{1}{3}$
1. $-3b - 15 \gt -24$
2. $-3b \gt -24 + 15$
3. $-3b \gt -9$
4. $b \lt -\frac{9}{3}$
5. $b \lt 3$

Intercepts

Intercepts in a graph refer to the points where a line or curve crosses the x-axis (x-intercept) or the y-axis (y-intercept). The x-intercept is the point where y = 0. The y-intercept is the point where x = 0.

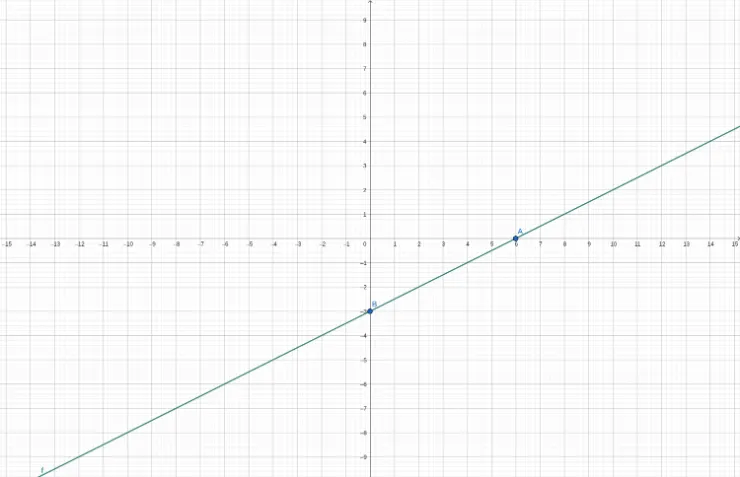
As you can see, the image above, A is the x-intercept because its y = 0, and B is the y-intercept because its x = 0. We can also see intercepts from the table.

$x$	$y$	$\Delta x$	$\Delta y$
0	-3	+2	+1
2	-2	+2	+1
4	-1	+2	+1
6	-0	+2	+1

Those intercepts are from the equation $y = \frac{1}{2}x - 3$, and here is how we calculate the equation to find the intercepts.

1. We start by setting $x = 0$ to find the y-intercept.
2. $y = \frac{1}{2}0 - 3$
3. $y = -3$
1. We start by setting $y = 0$ to find the x-intercept.
2. $0 = \frac{1}{2}x - 3$
3. $0 + 3 = \frac{1}{2}x$
4. $3 = \frac{1}{2}x$
5. $3 \times 2 = x$
6. $6 = x$

Slope

Slope refers to the steepness of a line and is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. Slope is often calculated as "rise over run," meaning the change in the y-coordinate (vertical change) divided by the change in the x-coordinate (horizontal change). Here is the equation to find the slope.

\[Slope = \frac{\text{Change in y}}{\text{Change in x}} = \frac{\Delta{y}}{\Delta{x}} = \frac{y2 - y1}{x2 - x1}\]

Slope-intercept Form

The slope-intercept form is a way to write the equation of a straight line. It is written as $y = mx + b$, where $m$ represents the slope of the line and $b$ represents the y-intercept.

The slope-intercept form of a linear equation is not attributed to a single individual but rather evolved through the work of several mathematicians. While René Descartes (1596–1650) is credited with developing the $x/y$ coordinate system and the concept of slope, the specific notation and formalization of the slope-intercept form, as we know it today, is attributed to Irish mathematicians like Matthew O'Brien (1844) and George Salmon (1855).

Functions

An equation is a statement that two expressions are equal, while a function is a specific type of relationship where each input has exactly one output. While some equations can represent functions, not all equations are functions, and vice versa.

	Equation	Function
Example	$3x + 5 = 20$	$f(x) = 3x + 5$
Purpose	To find values of variables that satisfy the equation.	To model the relationship between variables.
Form	Expression 1 = Expression 2	$f(x)$ = expression involving $x$
Solution	Has solutions (specific values of variables).	No solutions, but provides an output for each input.

References

Algebra (Part 1)