Algebra (Part 1)

I suggest you read my previous article about Pre-Algebra because we are going further. Let's become more serious about Algebra. Algebra is heavily used in Artificial Intelligence (AI). It is important to master Algebra if you want to master AI Engineering.

Compound Inequality

A compound inequality is a combination of two or more simple inequalities linked by the words "AND" or "OR". These inequalities can be graphed on a number line to visually represent the solution set. Here are examples.

\[x \lt 3 \text{ OR } x \gt 5\]

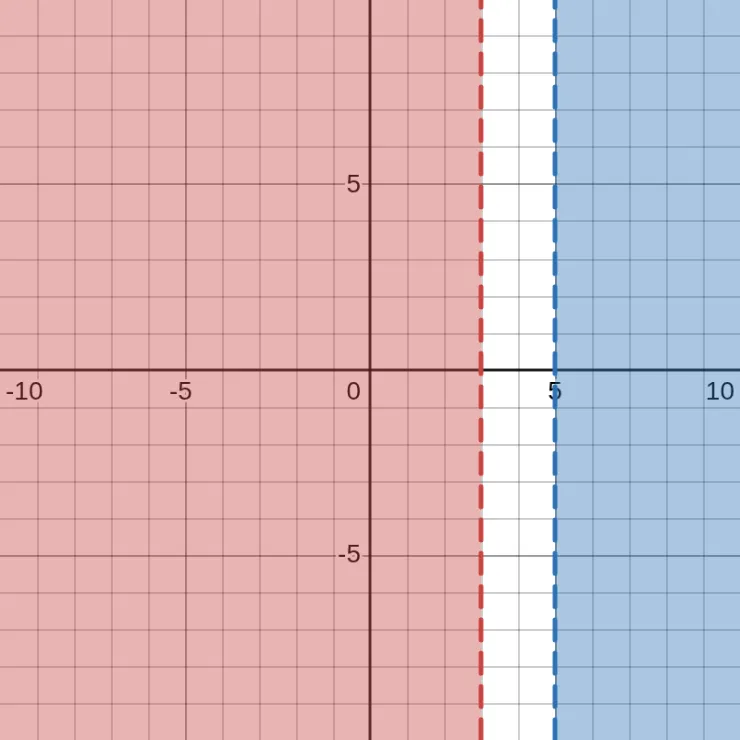
x < 3 OR x > 5
\(x \lt 3 \text{ OR } x \gt 5\). Red for \(x \lt 3\). Blue for \(x \gt 5\).

We use dashed lines to print \(\lt\) and \(\gt\).

\[x \le 3 \text{ OR } x \ge 5\]

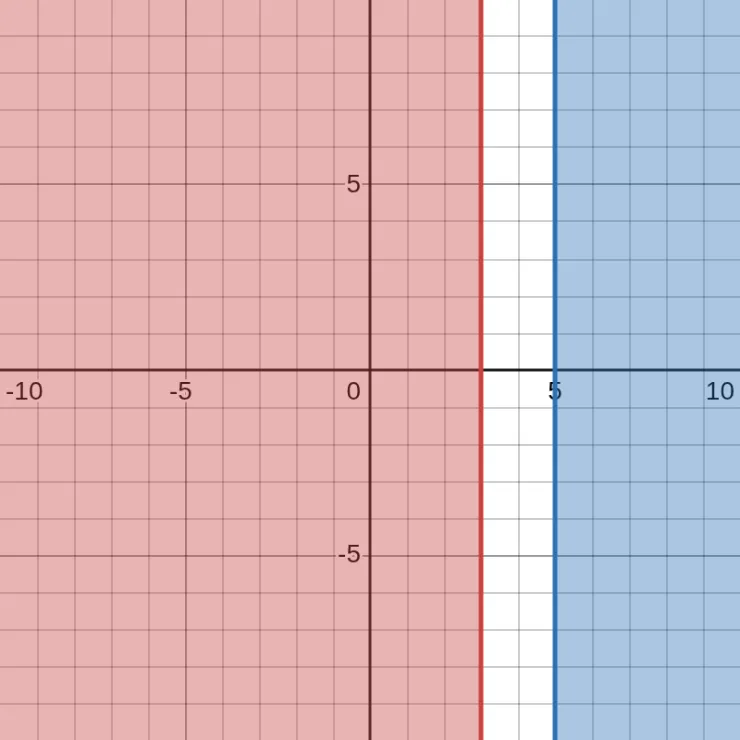
x ≤ 3 OR x ≥ 5
\(x \le 3 \text{ OR } x \ge 5\). Red for \(x \le 3\). Blue for \(x \ge 5\)

We use solid lines to print \(\le\) and \(\ge\).

\[x \gt 0 \text{ AND } x \lt 4\]

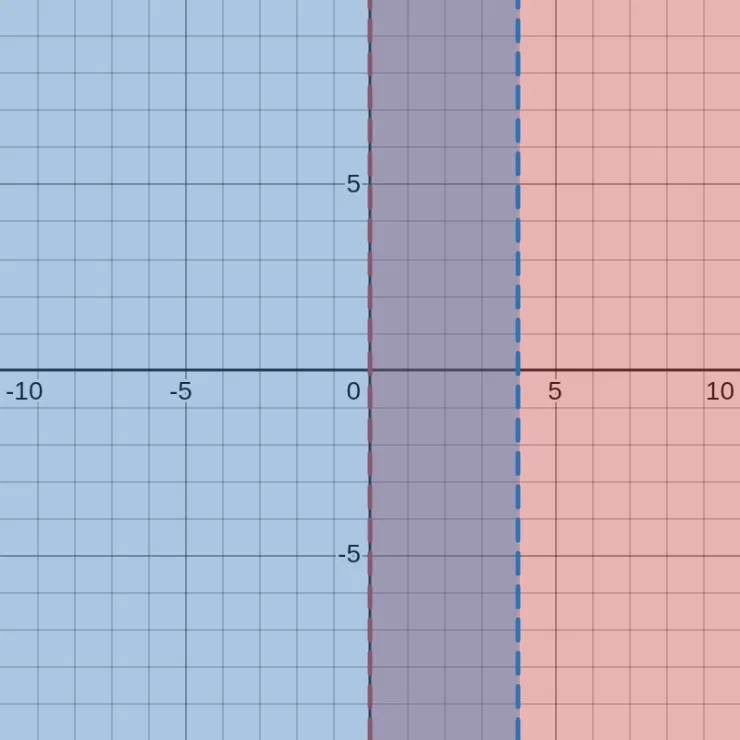
x > 0 AND x < 4
\(x \gt 0 \text{ AND } x \lt 4\). Red for \(x \gt 0\). Blue for \(x \lt 4\)

So, in this case, 1, 2, or 3 is a solution of the compound inequality, but -1, 0, 4, or 5 is not because it only satisfies one of the inequalities, not both.

We could also simplify \(x \gt 0 \text{ AND } x \lt 4\) to \(0 \lt x \lt 4\).

Simplify Compound Inequality

It's important to be able to simplify compound inequalities. Simple compound inequalities can make them easier to understand.

\[5x - 4 \ge 12 \text{ OR } 12x + 5 \le -4\]
  1. \(5x - 4 \ge 12\)
  2. \(5x \ge 12 + 4\)
  3. \(5x \ge 16\)
  4. \(x \ge \frac{16}{5}\)
  1. \(12x + 5 \le -4\)
  2. \(12x \le -4 - 5\)
  3. \(12x \le -9\)
  4. \(x \le -\frac{9}{12}\)
  5. \(x \le -\frac{3}{4}\)
\[x \ge \frac{16}{5} \text{ OR } x \le -\frac{3}{4}\]
\[-7x - 50 \le -1 \text{ AND } -6x + 70 \gt -2\]
  1. \(-7x - 50 \le -1\)
  2. \(-7x \le -1 + 50\)
  3. \(-7x \le 49\)
  4. \(x \ge -\frac{49}{7}\)
  5. \(x \ge -7\)
  1. \(-6x + 70 \gt -2\)
  2. \(-6x \gt -2 - 70\)
  3. \(-6x \gt -72\)
  4. \(x \lt \frac{72}{6}\)
  5. \(x \lt 12\)
  1. \(x \ge -7 \text{ AND } x \lt 12\)
  2. \(-7 \le x \lt 12\)

Graphing Slope-intercept Form

In my previous article, Pre-Algebra, I already introduced equations of Slope and Slope-Intercept Form. Let's recap those equations by drawing graphs.

Remember that the line is always linear or straight. To draw a straight line, we need at least two points. Here is an example.

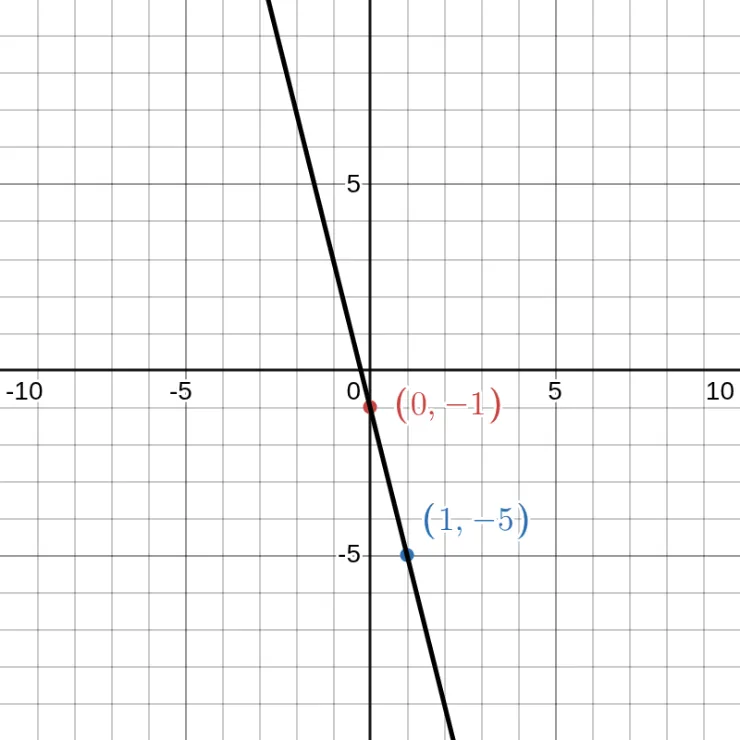
\[y = -4x - 1\]
\(x\) \(y\)
0 -1
1 -5

Now, we already have two points here (0, -1) and (1, -5). So, the graph will be like this.

y = -4x - 1
\(y = -4x - 1\)

Now, let's reverse. How about we have a graph, and we need to write the equation? Here is an example.

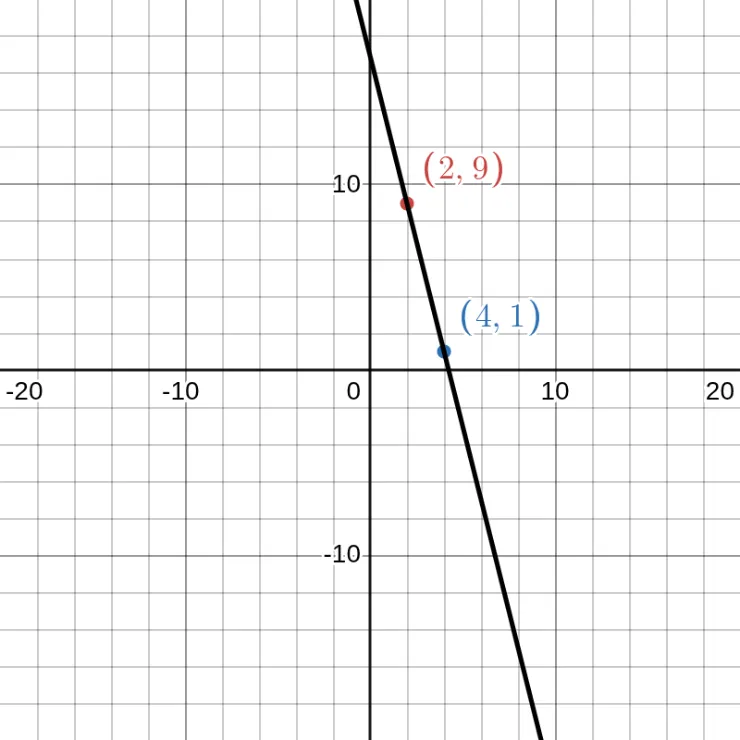
(2, 9) and (4, 1)
(2, 9) and (4, 1)

We have two points here: (2, 9) and (4, 1). We need to find the slope (\(m\)) first.

  1. \(m = \frac{\Delta y}{\Delta x}\)
  2. \(m = \frac{y2 - y1}{x2 - x1}\)
  3. \(m = \frac{1 - 9}{4 - 2}\)
  4. \(m = -\frac{8}{2}\)
  5. \(m = -4\)

We found that the slope of (2, 9) and (4, 1) is -4. Now, let's find the y-intercept (\(b\)).

  1. \(y = mx + b\)
  2. \(9 = -4 \cdot 2 + b\)
  3. \(9 = -8 + b\)
  4. \(8 + 9 = b\)
  5. \(17 = b\)

So, the answer is \(y = -4x + 17\).

Point-slope Form

Point-slope form is a way to represent the equation of a straight line using its slope and a point on the line.

\[y - b = m(x - a)\]

If we found a line that passes through (7, 3) whose slope is 2. Then \(m = 2\), \(a = 7\), and \(b = 3\). So, the point-slope form is \(y - 3 = 2(x - 7)\).

y - 3 = 2(x - 7)
\(y - 3 = 2(x - 7)\)

Standard Form

ax + by = c
\(ax + by = c\)

The standard form of a linear equation is \(ax + by = c\), where a, b, and c are real numbers.

As an example, let's say we have \(5x - 2y = 10\). Let's find the two points from this equation.

\[5x - 2y = 10\]
\(x\) \(y\)
0
  1. \(5x - 2y = 10\)
  2. \(5 \cdot 0 - 2y = 10\)
  3. \(- 2y = 10\)
  4. \(y = -\frac{10}{2}\)
  5. \(y = -5\)
  1. \(5x - 2y = 10\)
  2. \(5x - 2 \cdot 0 = 10\)
  3. \(5x = 10\)
  4. \(x = \frac{10}{5}\)
  5. \(x = 2\)
 0

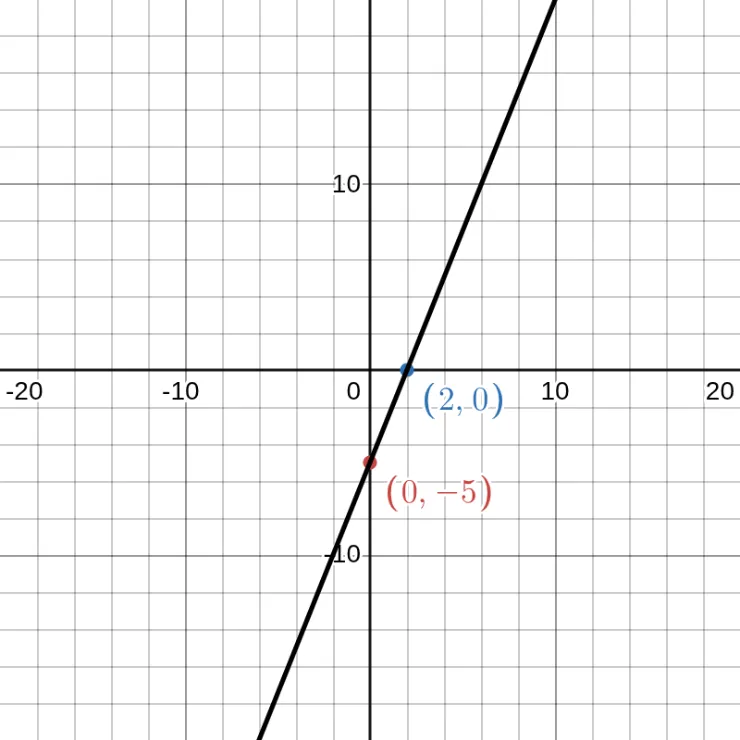
We already got two points from \(5x - 2y = 10\), they are (0, -5) and (2, 0). Let's draw the graph.

5x - 2y = 10
\(5x - 2y = 10\)

System of Equations

A system of equations is a set of two or more equations that are considered together because they involve the same variables. The goal is to find values for the variables that satisfy all equations in the system simultaneously. These systems can be linear or nonlinear and are used to model relationships between multiple variables.

There are several methods to solve systems of equations: Substitution, Elimination, Graphing, and Matrices. Here are examples for substitution and elimination.

Substitution Method

  1. \(-5x + 4y = 3\)
  2. \(-5 \cdot (2y - 15) + 4y = 3\)
  3. \(-10y + 75 + 4y = 3\)
  4. \(-10y + 4y = 3 - 75\)
  5. \(-6y = -72\)
  6. \(y = \frac{-72}{-6}\)
  7. \(y = 12\)
  1. \(x = 2y - 15\)
  2. \(x = 2 \cdot 12 - 15\)
  3. \(x = 24 - 15\)
  4. \(x = 9\)

Elimination Method

We need to multiply \(-2y + 3x = 4\) by 5 to get \(-10y + 15x = 20\). They are equivalent, but we can eliminate the \(y\) term by adding it with \(10y + 11x = -4\).

  1. \( \begin{aligned} 10y - 11x = -4 \\ -2y + 3x = 4 \\ \end{aligned} \)
  2. \( \begin{aligned} 10y - 11x = -4 \\ 5 \cdot (-2y + 3x = 4) \\ \end{aligned} \)
  3. \( \begin{aligned} 10y - 11x = -4 \\ -10y + 15x = 20 \\ \end{aligned} \)
  4. \( \begin{aligned} 10y - 11x = -4 \\ +~-10y + 15x = 20 \\ \hline \\ 4x = 16 \end{aligned} \)
  5. \(x = \frac{16}{4}\)
  6. \(x = 4\)
  1. \(-2y + 3x = 4\)
  2. \(-2y + 3 \cdot 4 = 4\)
  3. \(-2y + 12 = 4\)
  4. \(-2y = 4 - 12\)
  5. \(-2y = -8\)
  6. \(y = \frac{-8}{-2}\)
  7. \(y = 4\)

Number of solutions to system of equations

A system of linear equations mostly has a single solution, but sometimes it can have no solution (parallel lines) or infinite solutions (same line).

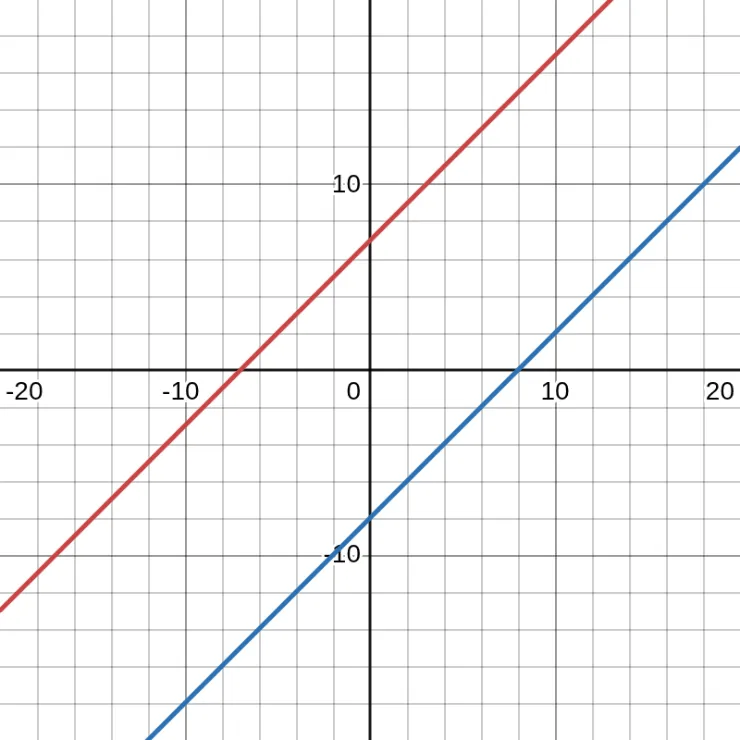
No Solution

If you see that they have the same slope, this means that they have no solution and they have parallel lines.

Parallel Lines. Red is y = x + 7. Blue is y = x - 8.
Parallel Lines. Red is \(y = x + 7\). Blue is \(y = x - 8\).

Infinite Solutions

If we divide \(7y = -14x + 28\) by 7, we will get \(y = -2x + 4\). They are the same. It means that they have infinite solutions and they are on the same line.

References

Related Articles