Algebra (Part 3)
In Pre-Algebra, we introduced variables, terms, factors, and coefficients. In short, a polynomial is a combination of terms. Here are examples.
- Monomial: \(3n^2\) (one term)
- Binomial: \(4t - 7\) (two terms)
- Trinomial: \(7x^3 + 8x + 9\) (three terms, and the highest degree is 3)
- Quadrinomial: \(6x^2 + 7x^3 + 8x^5 + 9\) (four terms, and the highest degree is 5)
- Quintinomial: \(x^4 + 2x^3 - 5x^2 + 7x - 1\) (five terms, and the highest degree is 4)
We can say that Binomial, Trinomial, Quadrinomial, Quintinomial, and beyond that are Polynomials.
The degree of the polynomial is the highest degree of its terms.
Multiplying Polynomials
By Monomial
Here are examples.
- \(4 \cdot 3x + 1 = 12x + 4\)
- \(4x \cdot 3x + 1 = 12x^2 + 4x\)
You could see that \(4 \cdot 3x = 12x\) and \(4x \cdot 3x = 12x^2\). Why did it get a second degree for \(4x \cdot 3x\)? That is because a general rule of the product of powers, \(a^m \cdot a^n = a^{m + n}\). Refers to Algebra (Part 2).
By Binomial
Here are examples.
- \(\begin{aligned} (x + 5)(x + 4)&=x^2 + 4x + 5x + 20 \\\\ &=x^2 + 9x + 20 \end{aligned}\)
- \(\begin{aligned} (x + 3)(x + 4)&=(x + 3)x + (x + 3)4 \\\\ &=x \cdot x + 3 \cdot x + x \cdot 4 + 3 \cdot 4 \\\\ &=x^2 + 3x + 4x + 12 \\\\ &=x^2 + 7x + 12 \end{aligned}\)
The second example above is provided for those who need more explanation. The first example has a short answer.
Binomial Special Products
Special binomial products are algebraic expressions that result from specific binomial multiplications.
Square of a Binomial
\[(a + b)^2 = a^2 + 2ab + b^2\]
\[(a - b)^2 = a^2 - 2ab + b^2\]
Product of a Sum and a Difference
\[(a + b)(a - b) = a^2 - b^2\]
Factors and Divisibility in Polynomials
Understanding factors and divisibility in polynomials is key to simplifying, solving, and analyzing algebraic expressions. In general, if \(p = q \cdot r\), then \(q\) and \(r\) are factors of \(p\) because \(p\) is divisible by \(q\) and \(r\). Here are examples.
- \(3x(x + 2) = 3x^2 + 6x\). \(x + 2\) is a factor of \(3x^2 + 6x\), and \(3x^2 + 6x\) is divisible by \(x + 2\).
- \((3x^2)(4x) = 12x^3\). \(3x^2\) is a factor of \(12x^3\), and \(12x^3\) is divisible by \(4x\).
Determining Factors and Divisibility
In general, if \(p\) divided by \(q\) results in a monomial with no remainder (i.e., no fractions or variables in the denominator), then \(q\) is a factor of \(p\).
- \(\begin{aligned} \frac{30x^4}{2x^2}&=\frac{30}{2} \cdot \frac{x^4}{x^2} \\\\ &=15 \cdot x^2 \\\\ &=15x^2 \text{ (monomial)} \\\\ &=30x^4 \text{ is divisible by } 2x^2 \end{aligned}\)
- \(\begin{aligned} \frac{6x}{12x^2}&=\frac{6}{12} \cdot \frac{x}{x^2} \\\\ &=\frac{1}{2} \cdot x^{-1} \\\\ &=\frac{1}{2} \cdot \frac{1}{x} \\\\ &=\frac{1}{2x} \text{ (not monomial)} \\\\ \end{aligned}\)
From the above, we can see that \(30x^4\) is divisible by \(2x^2\), but \(12x^2\) is not a factor of \(6x\) because \(x\) is in the denominator.
Factoring Trinomials
In general, to factor a trinomial of the form \(x^2+ bx + c\), we need to find factors of \(c\) that add up to \(b\). Here are examples.
- \(x^2 + 7x + 10 = (x + 2)(x + 5)\) because \(2 \cdot 5 = 10\) and \(2 + 5 = 7\).
- \(x^2 + 9x + 20 = (x + 5)(x + 4)\) because \(5 \cdot 4 = 20\) and \(5 + 4 = 9\).
Factoring by Grouping
Factoring by grouping is a technique used to factor polynomials with 4 or more terms. The idea is to group terms in pairs and factor each pair, then factor out the common binomial.
Here are the steps if we have a quadrinomial.
- \(ax + ay + bx + by\)
- \((ax + ay) + (bx + by)\)
- \((a + b)(x + y)\)
Here are examples.
- \(\begin{aligned} 3x^2 + 3x - 10x - 10&=(3x^2 + 3x)(-10x - 10) \\\\ &=3x(x + 1)-10(x + 1) \\\\ &=(3x - 10)(x + 1) \end{aligned}\)
- \(\begin{aligned} 2x^2 + 7x + 3&=2x^2 + 6x + x + 3 \\\\ &=(2x^2 + 6x)(x + 3) \\\\ &=2x(x + 3)+1(x+3) \\\\ &=(2x+1)(x+3) \end{aligned}\)
In general, we can factor a quadratic of the form \(ax^2 + bx + c\). The grouping method can be used to factor polynomials whenever a common factor exists between the groupings. For example, we cannot perform the grouping method on \(2x^2 + 7x + 12\) because we cannot find a common factor.
Why can we use Factoring by Grouping?
We want to factor a quadratic expression like \(ax^2+bx+c\) into two binomials \((Ax+B)(Cx+D)\). When we multiply \((Ax+B)(Cx+D)\), we get \(ACx^2+(AD+BC)x+BD\). This matches \(ax^2+bx+c\).
So:
- \(AC = a\)
- \(AD + BC = b\)
- \(BD = c\)
Now, define two numbers:
- \(m = BC\)
- \(n = AD\)
Then:
- \(m + n = b\)
- \(m \cdot n = a \cdot c\)
If you can find two numbers that add up to \(b\) and multiply to \(a \cdot c\), then you can split the middle term (\(bx\)) into \(mx + nx\) and use grouping to factor.
Difference of Squares
\[a^2 - b^2 = (a + b)(a - b)\]
Here are examples.
- \(x^2 - 25 = (x + 5)(x - 5)\)
- \(x^4 - 9 = (x^2 + 3)(x^2 - 3)\)
- \(4x^2 - 49y^2 = (2x + 7y)(2x - 7y)\)
Perfect Squares
\[a^2 + 2ab + b^2 = (a + b)^2\]
\[a^2 - 2ab + b^2 = (a - b)^2\]
We can use that equation if we find perfect squares in the first and last terms. Then the polynomial is a perfect square trinomial. Here are examples.
- \(\begin{aligned} 1 + 2x + x^2&=x^2 + 2x + 1 \\\\ &=(x)^2 + 2(x)(1) + (1)^2 \\\\ &=(x + 1)^2 \end{aligned}\)
- \(x^2 + 14x + 49 = (x + 7)^2\)
Summary of Factoring Quadratics
| Method | General Form | When is it applicable? |
|---|---|---|
| Factoring Out Common Factors | \(ax + bx = x(a + b)\) | Use when all terms share a common factor. |
| Sum-Product Pattern | \(x^2 + bx + c = (x + m)(x + n)\), where \(m + n = b\), \(mn = c\) | Use for trinomials of the form \(x^2+bx+c\), where you can find two numbers that multiply to \(c\) and add to \(b\). |
| Grouping Method | \(ax^2 + bx + c = (px + m)(qx + n)\) | Use for trinomials of the form \(ax^2+bx+c\) where \(a \ne 1\), and you can find two numbers that multiply to \(a \cdot c\) and add to \(b\). |
| Difference of Squares | \(a^2 - b^2 = (a - b)(a + b)\) | Use when the expression is a difference between two perfect squares. |
| Perfect Square Trinomials | \(a^2 + 2ab + b^2 = (a + b)^2\) | Use when the first and last terms are perfect squares, and the middle term is twice the product of their square roots. |
Quadratics by Taking Square Roots
Here's how to solve quadratic equations where the variable is raised to the power of two, by example.
\(\begin{aligned} x^2&=16 \\\\ \sqrt{x^2}&=\sqrt{16} \\\\ x&=\pm\sqrt{16} \\\\ x&=\pm4 \end{aligned}\)
\(\pm\) means either \(+\) or \(-\). So, \(\pm4\) means either \(4\) or \(-4\).
\(\begin{aligned} (x + 3)^2&=25 \\\\ \sqrt{(x + 3)^2}&=\sqrt{25} \\\\ x + 3&=\pm5 \\\\ x&=\pm5 - 3 \end{aligned}\)
\(\pm5 - 3\) means either \(5 - 3 = 2\) or \(-5 - 3 = -8\). So, \(\pm5 - 3\) means either \(2\) or \(-8\).
\[ax^2 + bx + c = 0\]
Here is an example of solving a general quadratic equation.
\(\begin{aligned} (x + 1)^2 - 36&=0 \\\\ (x + 1)^2&=36 \\\\ \sqrt{(x + 1)^2}&=\pm\sqrt{36} \\\\ x + 1&=\pm6 \\\\ x&=\pm6 - 1 \end{aligned}\)
So, we have two solutions here.
- \(x = 6 - 1 = 5\)
- \(x = -6 - 1 = -7\)
Let's check both solutions.
| \(x = 5\) | \(x = -7\) |
|---|---|
| \(\begin{aligned} (x + 1)^2 - 36&=0 \\\\ (5 + 1)^2 - 36&=0 \\\\ 6^2 - 36&=0 \\\\ 36 - 36&=0 \end{aligned}\) | \(\begin{aligned} (x + 1)^2 - 36&=0 \\\\ (-7 + 1)^2 - 36&=0 \\\\ -6^2 - 36&=0 \\\\ 36 - 36&=0 \end{aligned}\) |
Quadratics by Factoring
We just learned how to solve quadratic equations that include the variable raised to the second power by taking the square root of both sides. Now, let's learn how to solve factored quadratic equations and use factorization methods to solve other equations to a factored form and solve them.
Solving factored quadratic equations
Here are examples.
- \begin{aligned} (x+5)&(x+7)=0 \\\\ \swarrow\quad&\quad\searrow \\\\ x+5=0\quad&\quad x+7=0 \\\\ x=-5\quad&\quad x=-7 \end{aligned}
- \begin{aligned} (2x-1)&(4x-3)=0 \\\\ \swarrow\quad&\quad\searrow \\\\ 2x-1=0\quad&\quad 4x-3=0 \\\\ 2x=1\quad&\quad 4x=3 \\\\ x=\frac{1}{2}\quad&\quad x=\frac{3}{4} \end{aligned}
Using factorization methods to solve other equations
Here are examples.
- \begin{aligned} x^2-11x+28=(x-7)&(x-4)=0 \\\\ \swarrow\quad&\quad\searrow \\\\ x+5=0\quad&\quad x+7=0 \\\\ x=-5\quad&\quad x=-7 \end{aligned}
- \begin{aligned} 4x^2+4x+1=(2x+1)(2x+1)=0 \\\\ 2x+1=0 \\\\ 2x=-1 \\\\ x=-\frac{1}{2} \end{aligned}
- \begin{aligned} (x^2+3)^2&=4x^2+12 \\\\ x^4+6x^2+9&=4x^2+12 \\\\ x^4+6x^2+9-4x^2-12&=0 \\\\ x^4+2x^2-3&=0 \\\\ (x^2+3)(x^2-1)&=0 \\\\ \swarrow\quad&\quad\searrow \\\\ (x^2+3)&(x^2-1)=0 \\\\ x^2+3=0\quad&\quad x^2-1=0 \\\\ x^2=-3\quad&\quad x^2=1 \\\\ x=\pm i\sqrt{3}\quad&\quad x=\pm1 \end{aligned}
The example above shows how we transformed those equations into the factored form, and then we can find \(x\).
That \(i\) symbol means the imaginary unit. It means \(i\) is not a real number. It’s a new type of number introduced to make it possible to take square roots of negative numbers.
Quadratic Formula
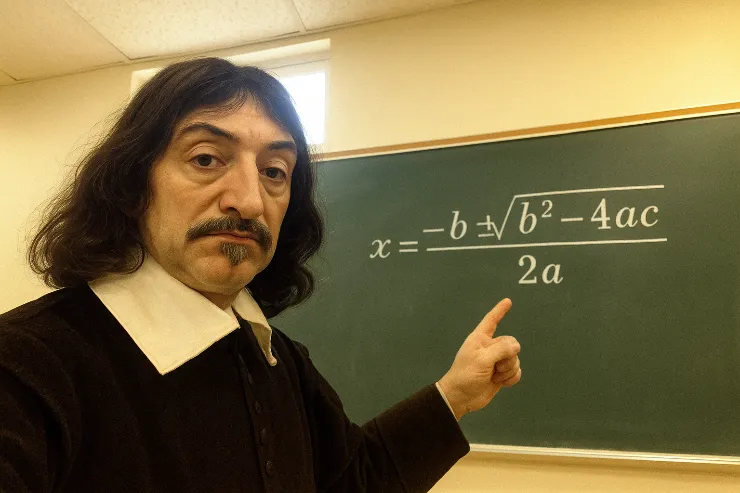
\[x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
The quadratic formula is used to find the solutions (roots) of a quadratic equation of the form \(ax^2 + bx + c = 0\). Here is an example.
\begin{aligned} 8x+10x^2-6&=17x \\\\ 8x-17x+10x^2-6&=0 \\\\ -9x+10x^2-6&=0 \\\\ 10x^2-9x-6&=0 \\\\ x&=\frac{-(-9)\pm\sqrt{(-9)^2-4(10)(-6)}}{2(10)} \\\\ x&=\frac{9\pm\sqrt{81-(-240)}}{20} \\\\ x&=\frac{9\pm\sqrt{321}}{20} \end{aligned}
Discriminant
\[x=\dfrac{-{b}\pm\sqrt{\color{gold}{b^2-4ac}}}{2a}\]
The discriminant helps determine the nature of the solutions:
- If the discriminant is positive, there are two distinct real solutions.
- If the discriminant is zero, there is exactly one real solution (a repeated root).
- If the discriminant is negative, there are two complex solutions (involving imaginary numbers).
From the example of the Quadratic Formula above, we can see that the discriminant is 321.
Proof
Here is proof that \(x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) is for \(ax^2 + bx + c = 0\).
- \[ax^2 + bx + c = 0\]
- \[x^2 + \frac{b}{a}x + \frac{c}{a} = 0\]
- \[x^2 + \frac{b}{a}x = -\frac{c}{a}\]
- \[x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} = -\frac{c}{a} + \frac{b^2}{4a^2}\]
- \[(x + \frac{b}{2a})^2 = \frac{b^2}{4a^2} - \frac{4ac}{4a^2}\]
- \[(x + \frac{b}{2a})^2 = \frac{b^2 - 4ac}{4a^2}\]
- \[x + \frac{b}{2a} = \pm\frac{\sqrt{b^2 - 4ac}}{2a}\]
- \[x = -\frac{b}{2a} \pm\frac{\sqrt{b^2 - 4ac}}{2a}\]
- \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Quadratics by Completing the Square
\[x^2 + 2ax + a^2\]
Solving quadratic equations by taking the square root or by factoring is relatively simple and efficient when applicable. Unfortunately, they are not always applicable. There is a method for solving any kind of quadratic equation. That method is called completing the square. I will explain it with an example.
How can we solve \(x^2 + 10x\)? The answer is easy by adding a coefficient of 10. Then, the expression will be \(x^2 + 10x + 25 = (x + 5)^2 = 0\).
The way we found 25 in \(x^2+10x\) is by \(\frac{10}{2} = 5\), then \(5^2 = 25\). \(x^2+{\color{gold}{10}}x\) is in the form of \(x^2 + {\color{gold}{2a}}x + a^2\). That's how we find \(a\) by dividing the number by 2, then squaring it (because the missing constant is \(a^2\)).
\[(x + a)^2 + b\]
\[(x + a)^2 = x^2 + 2ax + a^2\]
Here are more examples with that method to solve equations.
- \begin{aligned} x^2-8x&=5 \\\\ x^2-8x+16&=5+16 \\\\ x^2-8x+16&=21 \\\\ (x-4)^2&=21 \\\\ x-4&=\pm\sqrt{21} \\\\ x&=4\pm\sqrt{21} \end{aligned}
- \begin{aligned} 4x^2+20x-3&=0 \\\\ 4x^2+20x&=3 \\\\ 4(x^2+5x)&=3 \\\\ 4(x^2+5x+\frac{25}{4})&=3+4\cdot\frac{25}{4} \\\\ 4(x^2+5x+\frac{25}{4})&=3+25 \\\\ 4(x^2+5x+\frac{25}{4})&=28 \\\\ 4(x+\frac{5}{2})^2&=28 \\\\ (x+\frac{5}{2})^2&=\frac{28}{4} \\\\ (x+\frac{5}{2})^2&=7 \\\\ x+\frac{5}{2}&=\pm\sqrt{7} \\\\ x&=-\frac{5}{2}\pm\sqrt{7} \end{aligned}
Graphing Quadratics
The graph of a quadratic function is a parabola, a "u"-shaped curve.
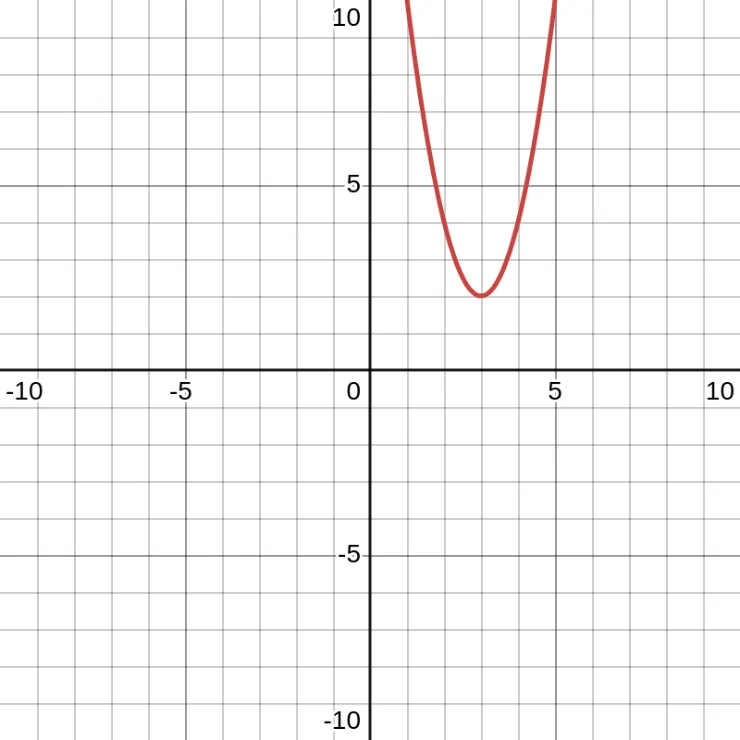
Vertex Form
\[y = a(x + h)^2 + k\]
- Vertex = \((h,k)\) directly from the equation.
- \(a\) = direction and width of parabola.
You can start at the vertex and use \(a\) to plot points symmetrically, no need to calculate the vertex.
Here is an example of \(y=2(x-3)^2+2\).
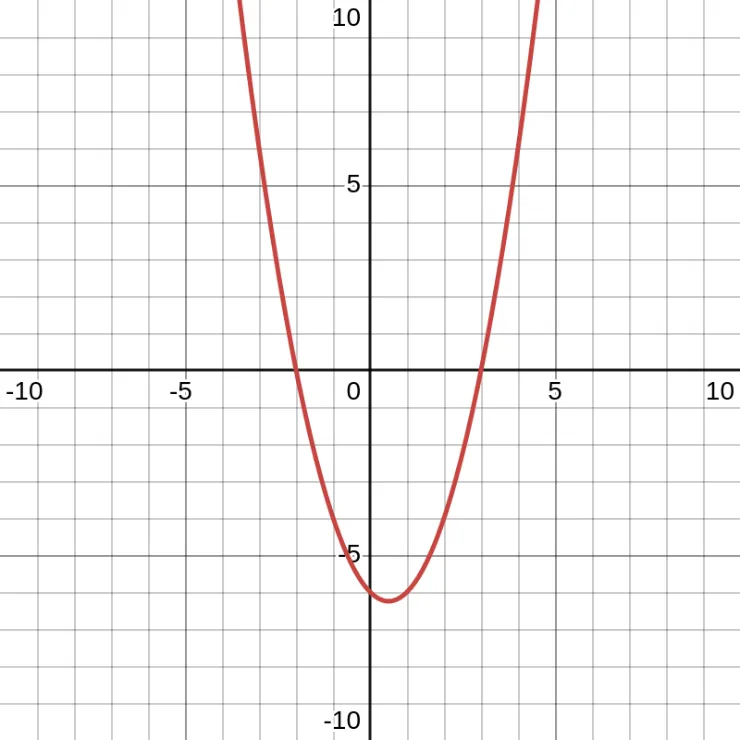
Non-Vertex Form
Here is an example of \(y = x^2 - x - 6\) (Standard Form).
\[x = -\frac{b}{2a}\]
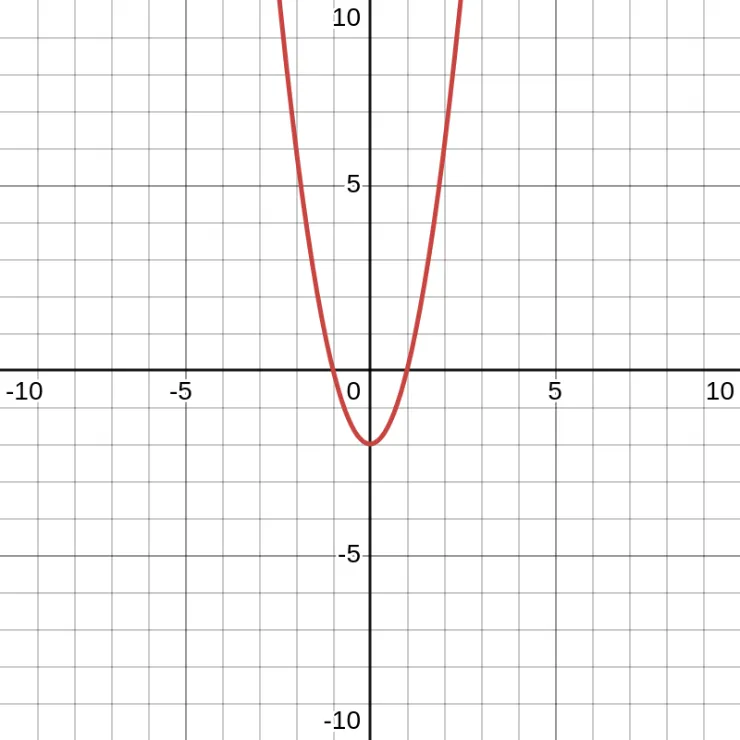
Here is an example of \(y = 2(x+1)(x-1)\) (Factored Form).
\[x = \frac{r_1 + r_2}{2}\]
Irrational Numbers
An irrational number is a real number that cannot be expressed as a simple fraction (a ratio of two integers, a/b). In decimal form, irrational numbers have infinite non-repeating decimal expansions. Here are examples.
- The square root of 2. \(\sqrt{2} \approx 1.414213\ldots\)
- Pi. \(\pi \approx 3.141592\ldots\)
- Euler's number. \(e \approx 2.718281\ldots\)
Reference
The main reference of this article is from Khan Academy.