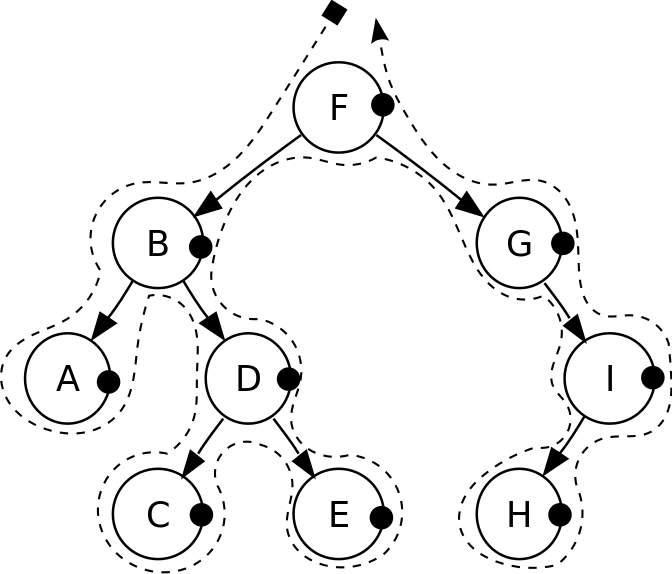
Binary Tree
Binary Tree is a non-linear data structure. It is made up of nodes. Each node can hold a maximum of two nodes, Left and Right. It is to represent hierarchical information.
A node that has no parent is called Root. A link from parent to a child node is called Edge. A node that has the same level as some nodes are called Sibling. A node that has no children is called Leaf.
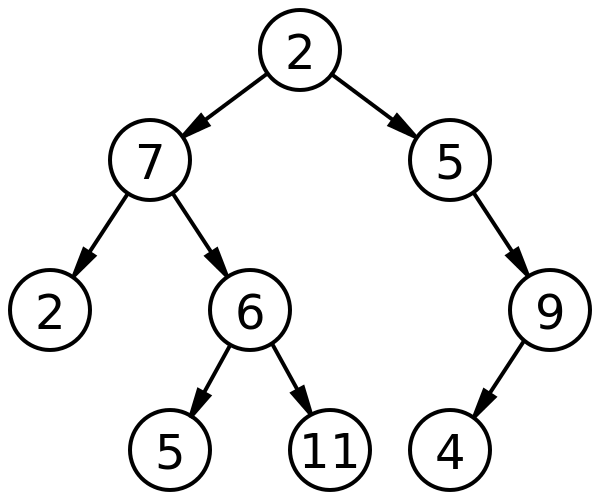
Traversal
Visiting every node is called Traversal. There are two order types; Breadth-First and Depth-First.
Breadth-First
Visiting every node at the same level before moving to the next level.
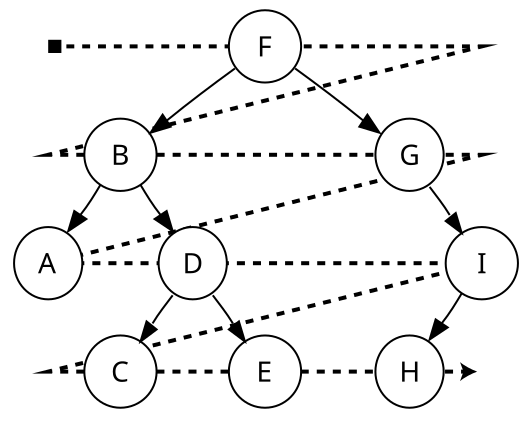
Depth-First
Visiting every node with going deep to the leaf before moving to the next node of the same level and can be performed in three ways; Pre-Order, In-Order, and Post-Order.
Pre-Order
The left subtree has processed before the right subtree.

In-Order
Similar to Pre-Order. But, start from the Leaf to the upper level of the node.

Post-Order
Similar to In-Order. But, instead of going to the upper level first, it is moving to the node of the same level first.